Tiago Charters work gallery about contact

Uma das formas de gerar números com uma distribuição uniforme num intervalo é usando o método de congruências lineares¹. Vejamos então como implementar um gerador de números pseudo-aleatórios que gera números inteiros entre 0 e m com uma distribuição uniforme .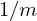

A ideia é gerar uma sucessão de números com a forma 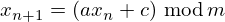onde²

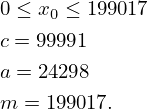
Ao valor de 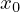dá-se o nome de semente porque é o primeiro termo da sucessão e é usado como input para o termo seguinte. Note-se que para um mesmo obtém-se sempre o mesmo .

A sucessão de números assim obtida tem período e o intervalo de variação dos valores da sucessão pode ser ajustado ao intervalo 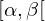através de

A maneira mais directa é escrever

(defun rand (a c m x)
  (mod (+ (* a x) c) m))

e obtém-se

> (rand 24298 99991 199017 0)

99991

Esta não é a maneira preferível de obter um número aleatório. Queremos obter um número simplesmente fazendo (rand), mas para isso, temos de ter uma maneira de guardar os sucessivos termos da sucessão de modo a que sirvam de sementes para os termos seguintes. Assim vamos definir a variável

(defvar *r-seed* 0)

que inicializa a sucessão de sementes (ou dos próprios números pseudo-aleatórios). Esta é uma variável global e por isso está enquadrada por *. Definimos um substituto para a função anterior como

(defun rand1 ()
  (let ((a 24298)
        (c 99991)
        (m 199017))
    (cond ((<= *r-seed*  199017)
           (setf *r-seed* (mod (+ (* a *r-seed*) c) m)))
          (t
           (setf *r-seed* 0)))))

onde agora os parâmetros a, c e m são locais e estão definidos dentro da função. Assim

> (rand1)

99991

A função rand1 é simples de perceber. Depois de inicializar as quantidades a, c e m verifica se *r-seed* é menor ou igual a 199017, se sim altera o valor de *r-seed* para o novo termo da sucessão através de

(setf *r-seed* (mod (+ (* a *r-seed*) c) m))

se não

(setf *r-seed* 0)

De modo a gerar números aleatórios entre 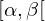define-se a função

(defun rand (&optional alpha beta)
  (let ((m 199017))
    (cond ((not (and alpha beta))
           (float (/ (rand1) m)))
          (t
           (+ (* (float (/ (rand1) m)) (- beta alpha)) alpha)))))

com dois argumentos opcionais alpha e beta; se não forem dados (rand) gera números com uma distribuição uniforme no intervalo :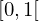

> (rand)

0.55237997

> (rand 0 2)

1.1378727

Ref:

1. D. Knuth, TAOCP

2. Master Library da TI Programable 58/59

---

For attribution, please cite this page as:

Charters, T., "Números pseudo-aleatórios em LISP": https://nexp.pt/rand.html (23-01-2025 [00:04])

---

(cc-by-sa) Tiago Charters - tiagocharters@nexp.pt