Placa ondulada

Cálculo do comprimento de uma placa ondulada através do cálculo de um integral elíptico

Exemplo de motivação, para a aula de hoje, para o cálculo de aproximações numéricas de integrais definidos.

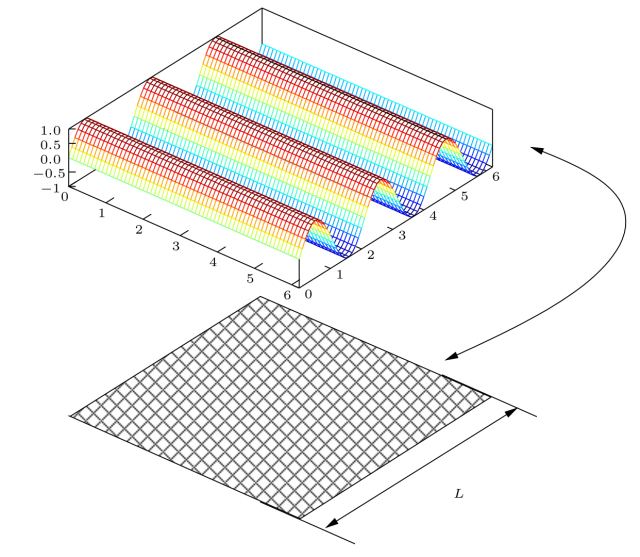
A figura mostra o gráfico da função 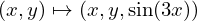$latex2png equation$ que modela uma placa ondulada obtida da deformação de uma placa de lado maior L.

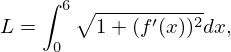
Quer saber-se qual o comprimento L da placa original de modo a que a placa ondulada tenha as dimensões da figura. O valor de L pode ser obtido através do cálculo do integral $latex2png equation$

onde 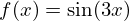$latex2png equation$ Ora acontece que este integral com esta escolha da função f é um integral elíptico que não pode ser expresso em termos de funções elementares (por funções elementares entendem-se as seguintes: polinómios, funções racionais, sin, cos, e^x, ln x, ...), a única forma de obter uma aproximação ao valor de L é usando um método numérico. Isso mesmo pode ser feito usando a instrução trapz em GNU/Octave

> x=linspace(0,6,10000);
  trapz(x,sqrt(1+9*cos(3*x).^2))
ans =  13.171

que calcula uma aproximação ao valor do integral dividindo o intervalo de integração, neste caso, em 10000 sub-intervalos e aproximando o valor de L através da soma das áreas dos trapézios formados com os extremos de cada sub-intervalo e as suas imagens.

A instrução seguinte mostra a convergência das sucessivas aproximações para o valor exacto onde a primeira coluna é o número de sub-intervalos considerados:

> for i=1:6; x=linspace(0,6,10^i);z(i)=trapz(x,sqrt(1+9*cos(3*x).^2));end;
> [10.^[1:6]' z']
ans =

                    10      13.4567198483149
                   100      13.1730277692198
                  1000      13.1711968984003
                 10000      13.1711789419263
                100000      13.1711787626897
               1000000      13.1711787608981

Palavras chave/keywords: Placa ondulada, matemática, GNU/Octave

Criado/Created: NaN

Última actualização/Last updated: 10-10-2022 [14:26]

Voltar à página inicial.