Interpolação fractal

A interpolação fractal consiste em construir uma função contínua que passa por um conjunto de pontos e cujo o gráfico é uma curva fractal

A interpolação fractal consiste em construir uma função contínua que passa por um conjunto de pontos e cujo o gráfico é uma curva fractal. A construção desta curva fractal é feita recorrendo a um sistema de funções iteradas (SFI) que de seguida se define como um conjunto de funções afins.

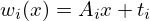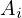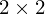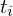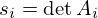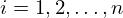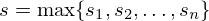Chama-se sistema de funções iteradas a um conjunto de aplicações afins $latex2png equation$ , , onde $latex2png equation$ é uma matriz $latex2png equation$ com entradas reais e $latex2png equation$ um vector coluna com entradas reais, com factor de contracção $latex2png equation$ , $latex2png equation$ . A contracção máxima deste conjunto de aplicações é dado pelo número $latex2png equation$ .

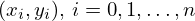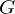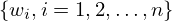Em geral para se construir o SFI que interpola o conjunto de pontos $latex2png equation$ cujo conjunto invariante $latex2png equation$ é gráfico de uma função contínua interpoladora, considere-se o SFI $latex2png equation$ onde as aplicações 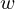$latex2png equation$ são definidas por

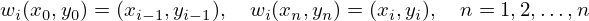
De modo a construir as aplicações que definem a função interpoladora é necessário impor-se as condições $latex2png equation$

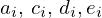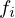
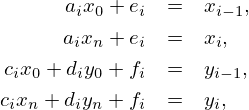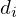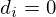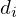Como cada aplicação é determinada pelos valores de $latex2png equation$ e $latex2png equation$ $latex2png equation$ que é um sistema linear sobre-determinado nos coeficientes da aplicação. Escolhe-se $latex2png equation$ como parâmetro livre. A escolha desta quantidade com parâmetro permite pondo $latex2png equation$ recuperar a forma da interpolação linear por troços. 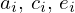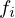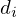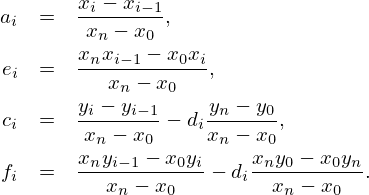Assim tomando $latex2png equation$ como parâmetro livre pode escrever-se cada uma das quantidades $latex2png equation$ e $latex2png equation$ em termos dos dados e de $latex2png equation$

$latex2png equation$

Ao parâmetro 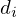$latex2png equation$ dá-se o nome de factor de escala.

A figura seguinte mostra exemplos de várias funções interpoladoras para alguns pontos sobre o gráfico da função seno para vários valores do factor contracção máxima (ver topo de cada gráfico, o vector d tem todas as componentes iguais a esse valor de contracção máximo em cada gráfico)

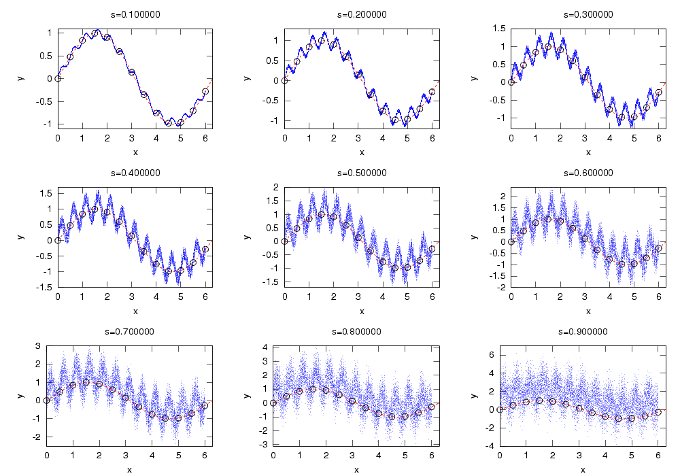
O código em GNU/Octave que permite gerar os pontos da função interpoladora fractal é

function [px py]=interpfrac(x,y,d,npoints)
  n=length(x);
  b=x(n)-x(1);

  for i=2:n
    aw(i-1)=(x(i)-x(i-1))/b;
    ew(i-1)=(x(n)*x(i-1)-x(1)*x(i))/b;
    cw(i-1)=(y(i)-y(i-1)-d(i)*(y(n)-y(1)))/b;
    fw(i-1)=(x(n)*y(i-1)-x(1)*y(i)-d(i)*(x(n)*y(1)-x(1)*y(n)))/b;
  endfor

  oldx=0;
  oldy=0;
  px=oldx;
  py=oldy;
  for j=1:npoints
    k=floor((n-1)*rand)+1;
    newx=aw(k)*oldx+ew(k);
    newy=cw(k)*oldx+d(k)*oldy+fw(k);
    oldx=newx;
    oldy=newy;
    px=[px; newx];
    py=[py; newy];
  endfor
endfunction

e para se obter os gráficos usa-se

x=[0:.5:2*pi];
y=sin(x);
t=[0:.01:2*pi];

clf
hold on

s=[.1:.1:.9];
for i=1:9
  d=s(i)*ones(1,length(x));
  subplot(3,3,i)
  hold on

  [xx, yy]=interpfrac(x,y,d,10000);
  plot(xx,yy,'.')
  plot(x,y,'ok')
  plot(t,sin(t),'r--')
  xlabel('x')
  ylabel('y')
  title(sprintf('s=%f',s(i)));
endfor;

Os gráficos seguintes mostram que variações se obtêm variando as diferentes entradas do vector d de uma forma aleatória num intervalo 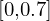$latex2png equation$ .

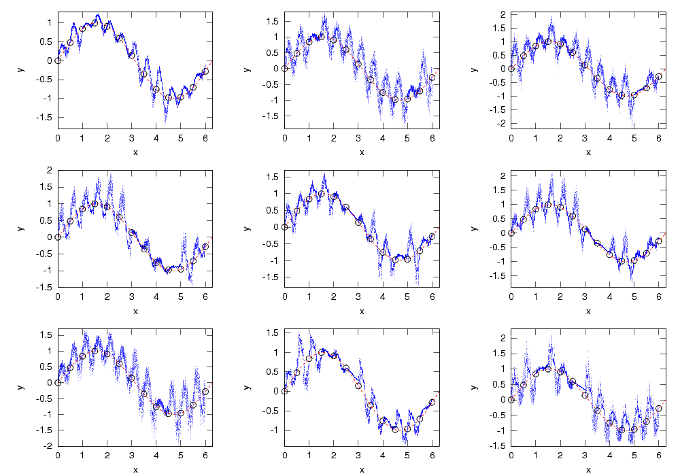
As instruções para os obter são

x=[0:.5:2*pi];
y=sin(x);
t=[0:.01:2*pi];

clf
hold on

for i=1:9
  d=.7*rand(1,length(x));
  subplot(3,3,i)
  hold on

  [xx, yy]=interpfrac(x,y,d,10000);
  plot(xx,yy,'.')
  plot(x,y,'ok')
  plot(t,sin(t),'r--')
  xlabel('x')
  ylabel('y')
endfor;

Palavras chave/keywords: fractal, interpolação, matemática, octave

Criado/Created: NaN

Última actualização/Last updated: 10-10-2022 [14:25]

Voltar à página inicial.