Tiago Charters work gallery about contact

I've used 16cm (outer diameter) PVC tubes. The 3D modeling was done using OpenScad and is under a GPLv3 license. Use the SCAD file to fit the vertices to any diameter tube.

Indoor geodesic dome (70cm radius)

For a 70cm radius we'll need 35cm tubes (30) and 45cm tubes (35). I'll put some math here in a couple of days (check the references below).

3D Printing

For a 2V geodesic dome we will need to print a total of 26 vertices

Number	Vertex type
10	4
6	5
10	6

Printer settings

res. = 0.32mm

infill = 20%

References

Geodesic Dome Notes and Calculator

OpenSCAD code

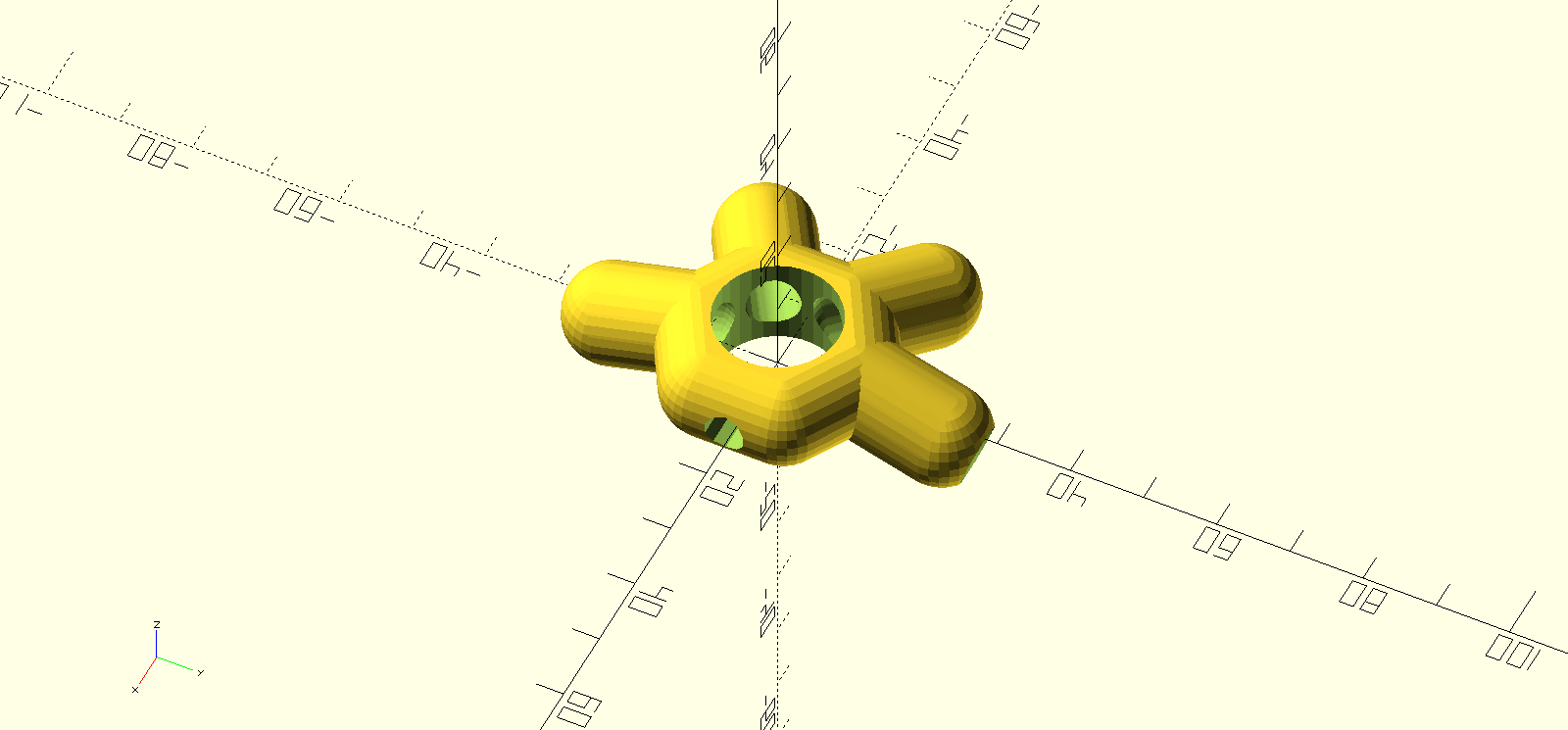
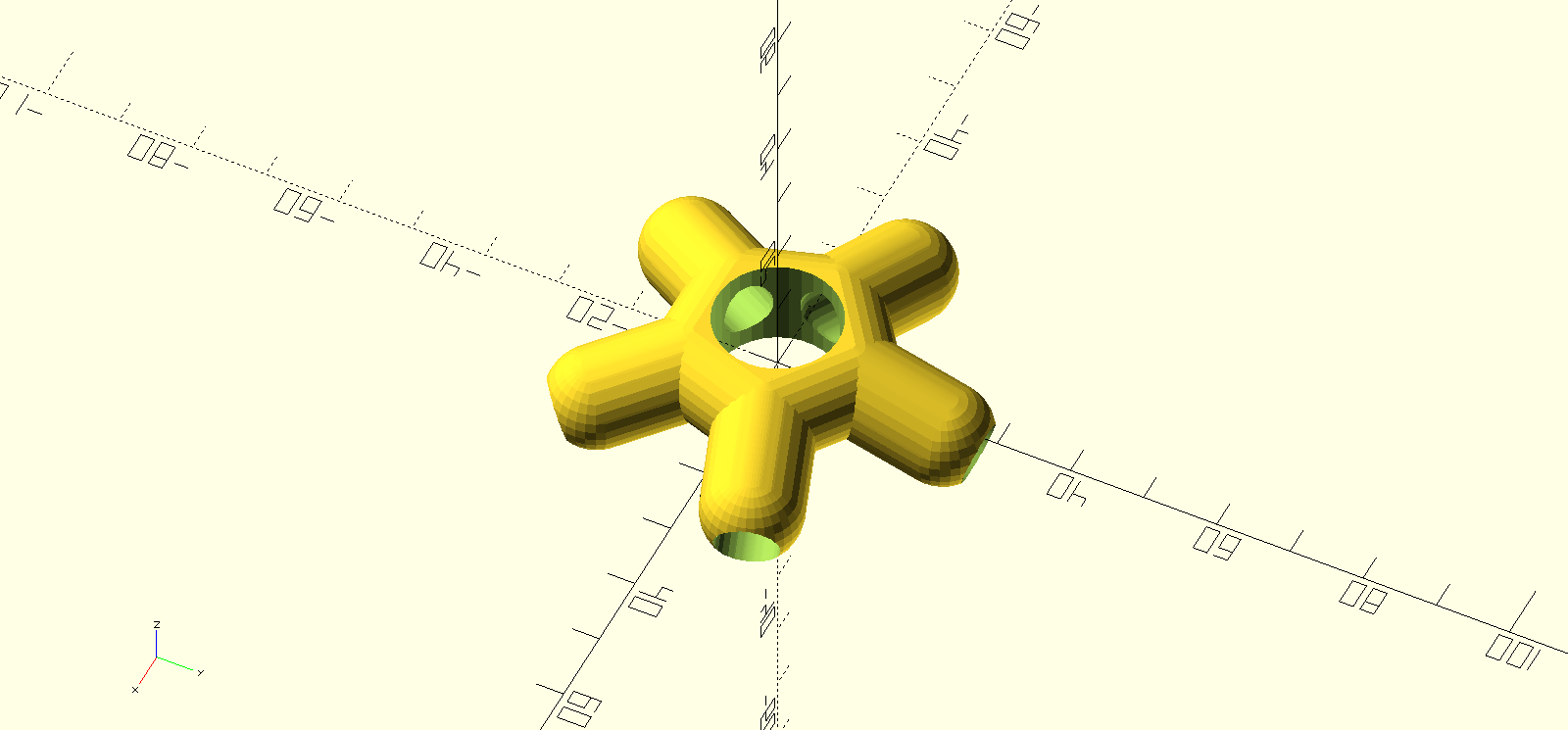
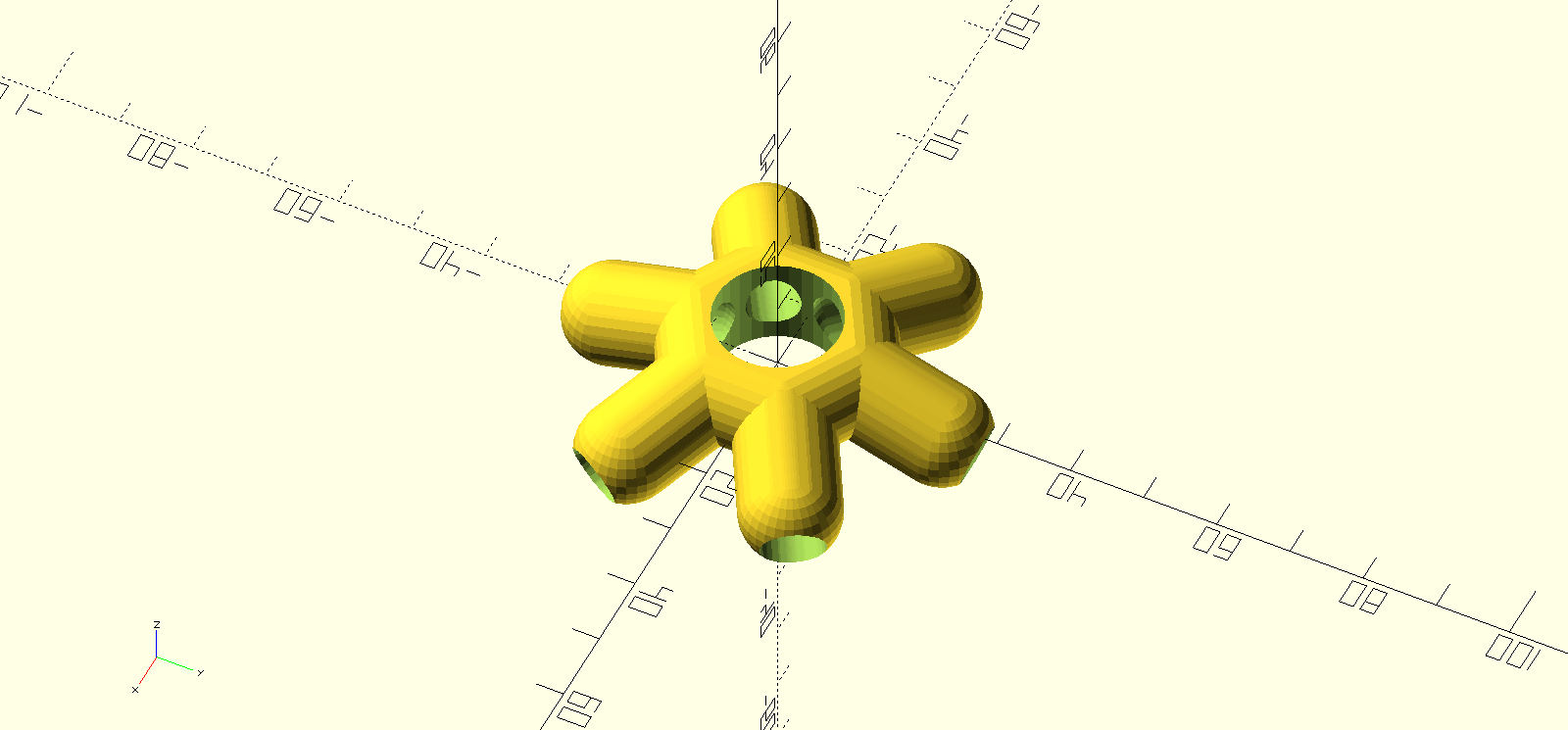
// Author: Tiago Charters de Azevedo
// Maintainer: Tiago Charters de Azevedo

// Copyright (c) - 2017 Tiago Charters de Azevedo (tca@diale.org)

// This program is free software; you can redistribute it and/or modify
// it under the terms of the GNU General Public License as published by
// the Free Software Foundation; either version 3, or (at your option)
// any later version.

// This program is distributed in the hope that it will be useful,
// but WITHOUT ANY WARRANTY; without even the implied warranty of
// MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
// GNU General Public License for more details.

// You should have received a copy of the GNU General Public License
// along with this program; if not, write to the Free Software
// Foundation, Inc., 51 Franklin Street, Fifth Floor,
// Boston, MA 02110-1301, USA.

// V2 dome vertices
// strut angle z axis
// https://simplydifferently.org/Geodesic_Dome_Notes?page=3#1V/L1%202/3%20Icosahedron%20Dome

// alpha1=15.86 (5 legs x6)
// alpha2=18.00 (6 legs x10)
// alpha2=18.00 (4 legs x10)

// Notes
//  Indoor r=70cm (door dimensions <=70cm)
// la=38.3cm
// lb=43.4cm
// A x 30: 0.54653 (15.86°)
// B x 35: 0.61803 (18.00°)

// ------------------------------------------------------------
// GNU GPL v2
// nop.head@gmail.com
// hydraraptor.blogspot.com
// See http://hydraraptor.blogspot.com/2011/02/polyholes.html
// ------------------------------------------------------------
function sides(r)=max(round(4*r),3);
function corrected_radius(r,n=0)=0.1+r/cos(180/(n ? n : sides(r)));
function corrected_diameter(d)=0.2+d/cos(180/sides(d/2));

module poly_circle(r,center=false){
    n=sides(r);
    circle(r=corrected_radius(r,n),$fn=n,center=center);}

module poly_cylinder(h,r,center=false){
    n=sides(r);
    cylinder(h=h,r=corrected_radius(r,n),$fn=n,center=center);}
// ------------------------------------------------------------

$fn=2*16;
phi=(1+sqrt(5))/2;
ri=13/2+.2; //PLA
ro=16/2+.1;
h=2*1.2;


module hub(n=5,m=5,ri=13.2/2,alpha=15.86,h=h){
    rm=1.5*ri;
    height=ri*sin(alpha);
    R=ri*cos(alpha);
    v=[0,R+rm,0]-[0,rm,height];
    difference(){
        union(){
            for(i=[0:m-1]){
                rotate([0,0,i*360/n]){
                    hull(){
                        translate([0,rm,height]){
                            sphere(ri,center=true);}
                        translate(v+[0,R+rm,0]){
                            sphere(ri,center=true);}}}}
            // Center
            hull(){
                for(i=[0:n]){
                    rotate([0,0,i*360/n]){
                        translate([0,rm,height]){
                            sphere(ri,center=true);}}}}}

        for(i=[0:m-1]){
            rotate([0,0,i*360/n]){
                hull(){
                    translate([0,rm,height]){
                        sphere(ri-h,center=true);}
                    v=[0,R+rm,0]-[0,rm,height];
                    translate(2*v+[0,R+rm,0]){
                        sphere(ri-h,center=true);}}}}
        // Center hole
        poly_cylinder(h=10*ri,r=ro,center=true);


        // Allow a nail to ground
        if(m==n-2){
            translate([1.5*ri,0,height])
            rotate([0,90,0]){
                poly_cylinder(h=3*ri,r=2.5+.15,center=true);}}
    }}



//Uncomment this
//hub(5,5,ri,15.86);
hub(6,6,ri,18.00);
//hub(6,4,ri,18.00);

Have fun!

---

For attribution, please cite this page as:

Charters, T., "FastDome": https://nexp.pt/fastdome.html (23-01-2025 [00:03])

---

(cc-by-sa) Tiago Charters - tiagocharters@nexp.pt