Tiago Charters Azevedo Index Faz qualquer coisa Dose Diária Recomendada Notas sobre diy

Métodos para equações não lineares

Calculo de raízes quadradas

Consideremos o problema de calcular a raiz quadrada de um número positivo 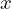, isto é, 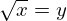tal qu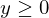e e 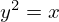. Tomando uma aproximação x para o valor da raiz quadrada de um número a, maior do que um, é fácil ver que (sqrt a) está entre x e a/x. Assim uma melhor aproximação ao valor da raiz quadrada de a será a média destas duas quantidades.

Consideremos o cálculo de 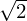. Tomando o valor 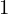como aproximação inicial, obtemos a tabela:

Aproximação         Quociente         Média

1                   2/1               (2+1)/2=1.5

1.5                 2/1.5=1.3333      (1.3333+1.5)/2=1.4167

1.4167              2/1.4167=1.4118   (1.4167+1.4118)/2=1.4142

1.4142              ...

Continuando com este processo iremos obter de cada vez melhores aproximações ao valor de 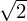. Este algoritmo na sua presente forma foi descoberto por Herão de Alexandria no século um A.C.

O procedimento anterior pode ser escrito como

(defun sqrt. (a x tol)
  (cond ((< (abs (- (* x x) a)) tol)
         x)
        (t
         (sqrt. a (* .5 (+ x (/ a x))) tol))))

Método da bissecção

O método da bissecção, também chamado método da divisão binária, é um dos métodos básicos para o cálculo de aproximações de soluções de equações não lineares 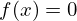onde 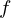é uma função contínua. É baseado no Teorema de Bolzano

Teorema de Bolzano

Seja uma função contínua no intervalo 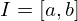, e 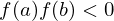então existe um 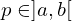tal que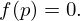

Este teorema garante a existência de pelo menos um zero da função 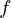no intervalo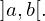

Comecemos então com a construção da primeira aproximação ao valor de p, i.e., a média m de a e b, (/ 2.0 (+ a b)) e calculemos o valor da função em a e em m, respectivamente fa e fm, através de (funcall f a) e (funcall f m). Assim o zero de f ou está na metade esquerda do intervalo I ou na metade direita. Se (> 0 (* fa fm)) é t então o zero que procuramos está na metade direita, caso contrário, está na metade esquerda. Assim voltamos a efectuar a divisão do intervalo com extremos m e b ou a e m, conforme o caso.

Claro que temos que controlar de alguma forma o número de aproximações que são calculadas, isso é feito calculando em cada aproximação o comprimento de cada intervalo, ou alternativamente, a distância entre duas aproximações sucessivas. O erro em cada aproximação m é metade do comprimento do intervalo e assim para um intervalo inicial de comprimento 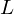e para um erro final 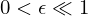teremos que efectuar 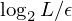iterações.

O procedimento que implementa este algoritmo é

(defun bisection (f a b)
  (let* ((m (/ (+ a b) 2.0))
        (fm (funcall f m))
        (fa (funcall f a)))
    (cond ((good-enough a b)
           m)
          (t
           (cond ((> (* fa fm) 0.0)
                  (bisection f m b))
                 (t
                  (bisection f a m)))))))

Para o controlo do erro em cada nova aproximação usamos um procedimento definido através da função good-enough. Temos duas maneiras diferentes de a definir em LISP.

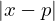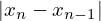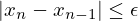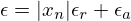Idealmente quer-se majorar o erro absoluto por uma quantidade pequena, no entanto o valor de do zero não é conhecido e, por isso, é usual substituir essa condição pela diferença em valor absoluto de duas aproximações sucessivas e pedir que onde e 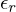, 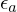são tolerâncias predefinidas com valor absoluto menor do que um (como segurança também se pode confirmar se a desigualdade se verifica para sucessivos aproximações). A escolha dos valores de 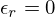ou 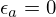tornam o critério de paragem, respectivamente, num critério que controla o erro absoluto ou o erro relativo. Pode também ter-se 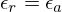o que faz com que, se 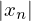for pequeno ou moderadamente grande, o controlo do erro seja efectuado pelo erro absoluto e, caso contrário se 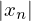for grande, o controlo nas sucessivas aproximações seja feito através do erro relativo.

O procedimento que implementa o controlo do erro é então dado por

(defun good-enough (x y eps-a eps-r)
  (< (abs (- x y)) (+ (* y eps-r) eps-a)))

Passar os valores de eps-a e eps-r como argumentos da função torna o código pouco elegante, podemos definir os valores destas quantidades como

(setq eps-r .0001
      eps-a 0.0)

e usar o scope sintáctico do LISP para recuperar o valor destas quantidades na chamada da função good-enough, que passamos a definir como

(defun good-enough (x y)
  (< (abs (- x y)) (+ (* y eps-r) eps-a)))

O procedimento sqrt. anterior pode agora também ser reescrito à custa de good-enough

(defun heron (a x)
  (cond ((good-enough (* x x) a)
         x)
        (t
         (heron a (/ (+ x (/ a x)) 2.0)))))

Ponto fixo

Um ponto fixo 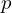de uma função 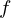é um número que satisfaz a equação 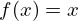. Sob certas condições é possível determinar um ponto fixo de uma função fazendo sucessivamente, a partir de uma aproximação inicial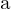

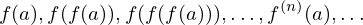até que se tenha aproximadamente 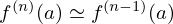. O procedimento seguinte implementa esta ideia

(defun fixed-point (op a)
  (let ((x (funcall op a)))
    (cond ((good-enough x a)
           x)
          (t
           (fixed-point op x)))))

Podemos usar o procedimento anterior para reescrever o procedimento que calcula a raiz quadrada de um número positivo

(defun sqrt. (a)
  (fixed-point (lambda (x) (/ 2.0 x (/ a x))) a))

Palavras chave/keywords: LISP, matemática, equações não lineares

---

Voltar à página inicial.

---

(c) Tiago Charters de Azevedo