Voo parabólico

Fazer uma previsão sobre o resultado final de uma epidemia como a que vivemos nestes dias pode ser visto como a determinação de um voo parabólico.

Uma bola atirada ao ar sujeita apenas ao seu próprio peso num campo gravítico constante descreve uma trajetória parabólica, é o que diz a nossa experiência diária à superfície da terra. O modelo matemático correspondente e que nos permite modelar e prever o movimento da bola é-nos dado pela física, pelas leis de movimento de Newton.

Imagine-se um jogo onde duas crianças atiram uma bola uma à outra. Para prevermos qual a trajetória dessa bola depois de lançada, diz-nos o modelo matemático validado pela experiência, que precisamos apenas de saber duas coisas para prever toda a trajetória da bola antes de ser agarrada no fim: onde estava a bola e qual a velocidade com que saiu das mãos do lançador quando a atirou, são as condições iniciais do lançamento. Como sabemos o valor da aceleração gravítica média à superfície da terra uma conta simples permite prever o futuro i.e. saber onde vai cair a bola e onde o jogador se tem que colocar para a receber.

Todos os dias, a meio do dia, recebemos o relatório da Direção Geral de Saúde sobre o desenvolvimento da epidemia do COVID19 em Portugal. Dois números são normalmente destacados nos órgãos de comunicação social e nas redes sociais. São eles o número total de infectados, N, e a variação desse número relativamente ao dia anterior, dN/dt¹. São números importantes, são duas quantidades relevantes para a descrição da propagação da epidemia porque a equação do movimento epidémica relaciona estas duas quantidades.

Porquê? Porque a solução desta equação permite fazer previsões sobre a dinâmica deste fenómeno que é um fenómeno natural. Porque existe uma lei do movimento para este tipo de fenómenos de crescimento no qual os acontecimentos epidemiológicos se enquadram. Não são os únicos. As curvas de evolução são curva-tipo-S, sigmóides: têm um crescimento rápido inicial e depois um plateau final, assimptótico. O modelo de evolução mais simples é o modelo logístico e permite fazer estimativas analíticas sobre o comportamento epidémico. Usualmente as previsões feitas com este modelo dão-nos um lower bound para a os parâmetros estimados².

A taxa de crescimento do número de infetados num dado dia é proporcional ao valor do número de infetados nesse dia. Isto acontece desde que o número de infetados se mantenha pequeno relativamente ao número total final de infetados. Este número total final de infetados é por agora desconhecido mas, à semelhança do voo parabólico da bola em que a altura máxima determina o valor final da distância percorrido, à medida que a epidemia se vai desenvolvendo mais perto estamos desse valor final. Enquanto estivermos longe desse dia a epidemia desenvolve-se num regime de crescimento (quasi)exponencial.

Quando o número de infetados num dia atinge os 10% do número total a evolução deixa de ser exponencial. A evolução continua a acelerar até atingir o máximo da taxa de infetados por dia e atinge um pico². A partir desse dia segue-se outro intervalo de tempo que nos leva aos 90% do número total de infetados. A duração d desse intervalo de tempo, que corresponde ao aumento de 10%-90%, é chamado tempo característico e depende unicamente do valor da taxa de crescimento exponencial k. É igual a ln(81)/k.

Atingido os 90% do número total de infetados a evolução estabiliza num plateau que corresponderá assimptoticamente ao número final de infetados.

E assim se constrói a curva-tipo-S.

É a propriedade do desenvolvimento parabólico da epidemia, o facto de que a metade do caminho podemos saber qual o número total de infetados, que nos permite prever ou estimar esse número final. Tal como a posição da bola no voo parabólico em que o ponto de altura máxima determina a distância total percorrida também o valor do número de infetados no momento onde a taxa número de infetados por dia é máxima determina o número final total de infetados. Aqui não temos força gravítica mas temos o número básico de reprodução que controla a taxa de crescimento exponencial da epidemia que é diferente, em geral, para diferentes vírus.

A figura seguinte mostra os dados oficiais do número de infetados em Portugal assim como o ajuste parabólico que se obtém pelo método dos mínimos quadrados. Sobreposto está também o comportamento esperado para a duração característica da epidemia.

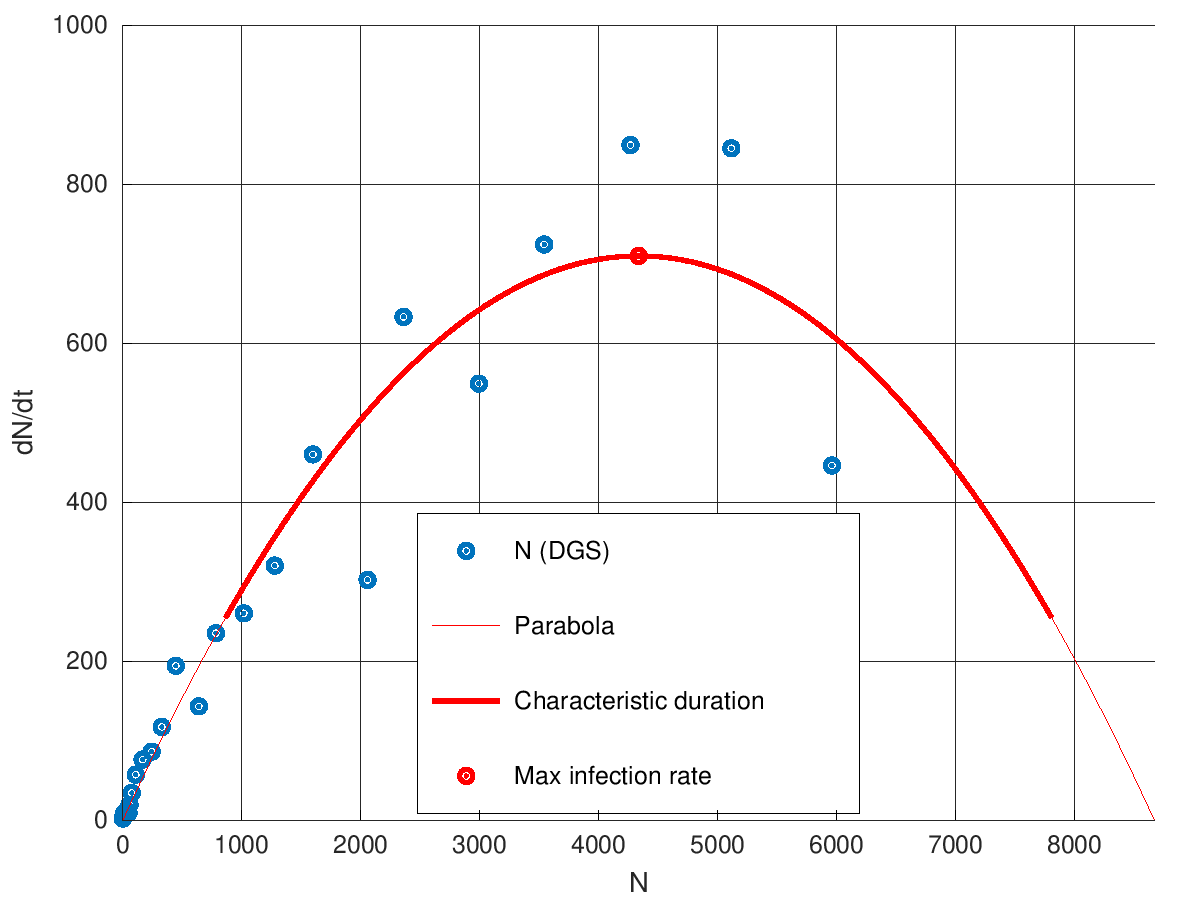
As conclusões são as seguintes e fáceis de retirar (30/03/2020):

taxa de infeção máxima 25 dias⁴ depois do primeiro contágio, já o ultrapassamos;
taxa de crescimento exponencial k igual a 0.32;
duração característica d de 13 dias;
número máximo de infetados M igual a 8676

E para que serve este texto? No fundo no fundo para pouco, para pensar no fenómeno natural a que por estes dias estamos sujeitos contra nossa vontade. Amanhã há mais novidades. Espero que melhores e tudo parece indicar que sim.

1. Sim, é a derivada, neste caso uma aproximação numérica.

2. Wuyue Yang, Dongyan Zhang, Liangrong Peng, Changjing Zhuge, Liu, Hong Rational evaluation of various epidemic models based on the COVID-19 data of China, (2020), arXiv:2003.05666

3. Formalmente é um máximo da primeira derivada. Não é o "pico" referido pela DGS.

4. Este dia é calculado pela expressão:

         1        No
t* = - -----*ln(------)
         k       M-No

onde No é o número inicial de infetados em Portugal, 2.

Criado/Created: 30-03-2020 [00:14]

Última actualização/Last updated: 27-11-2024 [17:00]

Back...

For attribution, please cite this work as:

Charters, T., "Voo parabólico": https://nexp.pt/ddr/parabolic.html (30-03-2020 [00:14])