Estranhamente não consegui encontrar uma conta

... simples com o resultado pelo qual o Malthus é tão adorado. Do ponto de vista formal o argumento é apenas uma verificação trivial do resultado que a função exponencial cresce mais depressa do que qualquer função polinomial.

O argumento básico de Malthus é simples. Se o número de indivíduos de uma determinada população duplicar, em pouco ciclos de duplicação ocupará toda a área que dispõe para viver.

Um modelo simples seria considerar que o número de indivíduos num instante n é dado por 2^n e a área ocupada n.

Basta mostrar assim que existe uma solução da equação não linear (em unidades adequadas) 2^n=a.n.

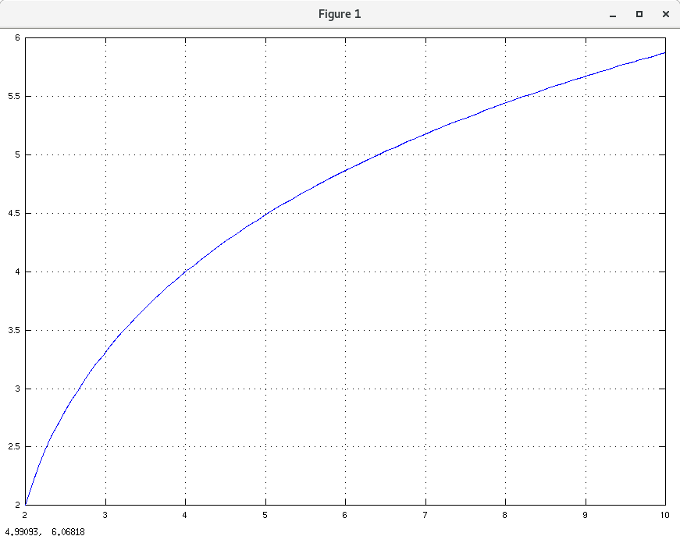
A solução é obtida resolvendo numericamente a equação e tem o gráfico que se mostra na imagem seguinte: o número de duplicações como função do parâmetro a (que depende do número inicial de indivíduos existentes e da área disponível).

A solução analítica obtém-se usando a função Lambert (todos temos funções preferidas a minha é esta função Lambert)

-1/log(2)*lambertw(-1,-log(2)./a)

E assim encontrei uma conta simples com o resultado pelo qual o Malthus é tão detestado.

Aqui fica o código em GNU/Octave para quem quiser brincar.

## Malthusian growth model

clear all

x=2;
m=10;

n=100;
amax=10;
a=linspace(2,amax,n);

for j=1:n
  for i=1:m
    x=x-(a(j)*x-2^x)/(a(j)-log(2)*2^x);
  end

  tend(j)=x;
end

clf
hold on
plot(a,tend,'-')
plot(a,-1/log(2)*lambertw(-1,-log(2)./a),'.r')
grid

Criado/Created: 24-08-2018 [22:00]

Última actualização/Last updated: 27-11-2024 [17:00]

Back...

For attribution, please cite this work as:

Charters, T., "Estranhamente não consegui encontrar uma conta": https://nexp.pt/ddr/malthus.html (24-08-2018 [22:00])