Não te fiques pelos ajustes

Este texto e os cálculos que apresento não correspondem a previsões oficiais e nem lhes devem ser dados a relevância que desejaríamos para tomada de decisões individuais. Correspondem simplesmente a um exercício que faço para compreender o problema e acompanhar a situação social em que nos encontramos e a propagação da epidemia em Portugal. É um exercício intelectual pessoal que me ajuda a viver durante estes dias de uma forma mais saudável. Há quem faça bolos ou arrume gavetas para se acalmar, eu faço contas.

Estamos habituados à ideia de crescimento até um certo limite, algo cresce e depois para. Há muitos exemplos de curvas de crescimento com forma de S. Podemos encontrar esta curva em muitos fenómenos diferentes: na evolução de número de indivíduos em populações de animais, humanos incluídos, utilização de fontes de energia, transportes e serviços, aprendizagem de línguas ou desempenho e utilização de tecnologias ou propagação de uma infeção viral como aquela que vivemos nestes dias.

Muitas vezes o tamanho de uma planta, ou de um número elementos de uma espécie animal numa determinada região, cresce exponencialmente, mas isso só ocorre no início desse crescimento. Este tipo de crescimento exponencial não ocorre sempre porque estes sistemas possuem um sistema de feedback negativo, um mecanismo pelo qual o processo de crescimento é atenuado por fatores externos, no caso da planta a falta de nutrientes no solo ou no caso de uma população animal o alimento ou restrições de espaço físico, ou internos, como o controlo da temperatura corporal nos mamíferos.

Claro que existem outros tipos de sistemas que têm um comportamento de crescimento mais complexo mas o crescimento logístico com uma curva em forma de S retrata bem a nossa intuição quando falamos sobre coisas ou fenómenos que crescem até uma determinada altura e depois param.

Os modelos matemáticos usados para descrever este tipo de crescimento são baseados em equações diferenciais ordinárias (EDO). A física usa equações deste tipo e.g. para modelar a trajetória de um corpo em movimento, as órbitas de planetas, etc, ... A 2ª lei de Newton define uma equação diferencial. Estas equações quando aplicadas ao crescimento de populações, à utilização tecnologia ou epidemias, descrevem o comportamento destes fenómenos em termos de trajetórias de crescimento contínuo e embora a população de humanos à superfície da terra ou o número de infetados por uma epidemia não seja uma variável contínua, são varáveis discretas, os modelos matemáticos contínuos são usados para modelação destes fenómenos por serem simples e fáceis de tratar analítica e numericamente.

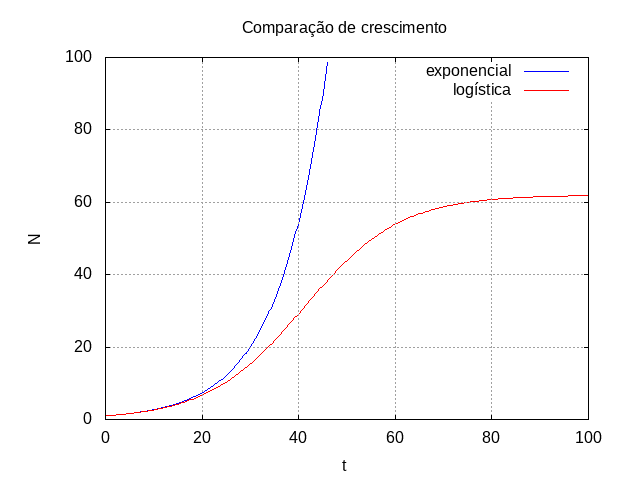
O crescimento exponencial é bem ilustrado pelo crescimento de populações de bactérias e que aumenta sem limite havendo espaço e alimento suficiente. A figura seguinte¹ mostra esse crescimento exponencial na curva azul.

A taxa de crescimento do número de bactérias num instante t, é proporcional ao número de bactérias N(t) nesse instante i.e. a variação do número de bactérias por unidade de tempo é proporcional ao número de bactérias que já existem (na realidade este modelo simples pode contabilizar numa única constante a taxa de "nascimentos" como a taxa de óbitos). A taxa de crescimento num instante t é a derivada de N(t) em ordem ao tempo.

A equação do crescimento exponencial pode ser escrita como

d N(t)
------ = k*N(t)
 d t

e cuja solução pode ser escrita usando o número de Nepper, exp~2.71...

N(t) = No*exp(k*t)

onde No é o número inicial de bactérias e k é a taxa de crescimento. Se quisermos saber qual o tempo T associado à duplicação do número de bactérias temos de resolver a equação

exp(k*t)=2^(t/T)

o que dá

T=ln(2)/k

Porque poucos sistemas, ou mesmo nada cresce indefinidamente, a equação do crescimento exponencial tem de ser modificada se quisermos modelar crescimentos com curvas de evolução em forma de S (ver curva a vermelho na figura anterior).

A modificação mais simples ao modelo de crescimento exponencial, e por isso uma das mais usadas, é o modelo logístico. Foi popularizado pelo biólogo Lotka nos anos 20 do século passado. O trabalho de Thornton de 1922² é um magnífico exemplo deste tipos de estudos aplicado à biologia e cujo resultado é este:

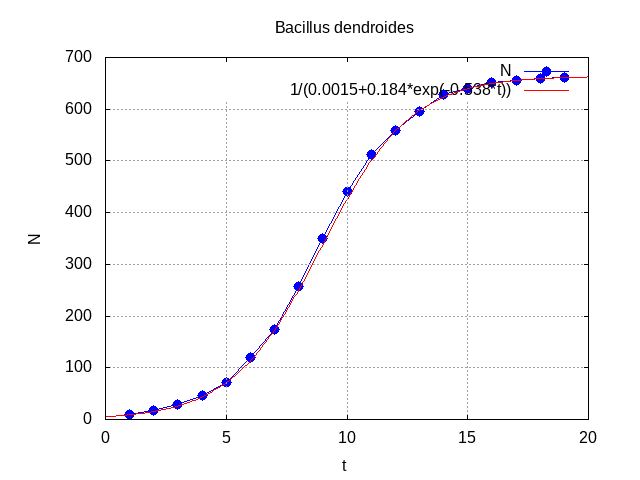
Fantástico!

O modelo logístico é relativamente fácil de perceber tomando como base o modelo exponencial.

A taxa de crescimento do modelo logístico começa por ser proporcional ao número N(t), com constante k, mas tem um termo de feedback negativo M-N(t) que faz abrandar o crescimento à medida que N(t) se aproxima do seu valor máximo assimptótico M. A equação diferencial completa fica assim com a forma

d N(t)
------ = r*N(t)*(M-N(t))
 d t

Note-se que o termo de feedback M-N(t) está próximo de 1 para valores de N(t)<<M e aproxima-se de 0 quando N(t)~M i.e. a taxa de crescimento começa por ser exponencial mas depois torna-se cada vez mais pequena à medida que N(t) se aproxima do seu valor máximo, produzindo assim um gráfico de N(t) em função do tempo com uma forma de S (curva a vermelho na imagem anterior).

Claro que, à semelhança do modelo exponencial e apesar da EDO ser não linear, é possível obter uma fórmula para a solução do modelo logístico³. É dada por

                 M*No
N(t) = ---------------------------, k=r*M, No, M>0
        No+(M-No)*exp(-r*M*(t-to))

onde to é um instante inicial, usualmente igual a zero, o início da contagem do tempo.

Outra forma mais apelativa

                M
N(t) = --------------------
        1+exp(-r*M*(t-t*))

onde t* é o instante onde a taxa de crescimento é máxima e é dado por

            1        No
t* = to - -----*ln(------)
           r*M      M-No

A primeira coisa que podemos afirmar, comparando as fórmulas para os dois casos, é que, escolhendo No, o modelo logístico possui dois parâmetros arbitrários que podem ser escolhidos dos três que estão na equação, a saber r, M e t*. Sabendo dois determinamos o terceiro. Vejamos então qual o significado de cada um:

r*M: é igual à taxa (inicial) de crescimento exponencial k, logo r será a taxa de crescimento por elemento da população, controla a "rapidez" com que N "descola" do seu valor inicial No;
M: valor final máximo assimptótico;
t* instante onde a taxa de crescimento é máxima. Prova-se que nesse instante o valor de N é igual a M/2 (segunda derivada nula).

Um outro parâmetro útil que define um tempo característico associado ao crescimento logístico é dado por

     ln(81)
d = -------
       k

Mede o tempo decorrido na variação de 10% a 90% no crescimento. Um intervalo de comprimento d pode ser colocado centrado em t*.

Bom, voltemos ao objetivo deste texto e explicar como podemos usar as ideias para descrever a propagação do número de infetados COVID19.

Há 19 dias foi detetado o primeiro caso de infeção COVID19. A série de temporal é a seguinte (volto a usar o Maxima) e é-nos dada diariamente pela Direção Geral de Saúde.

y:matrix(
  [0,2],
  [1,4],
  [2,6],
  [3,9],
  [4,13],
  [5,21],
  [6,30],
  [7,39],
  [8,(41+59)/2], /*quebra da série*/
  [9,59],
  [10,78],
  [11,112],
  [12,169],
  [13,245],
  [14,331],
  [15,448],
  [16,642],
  [17,785],
  [18,1020],
  [19,1298])$

Note-se que a nona observação, onde a hora do dia foi alterada para comunicação dos dados oficiais, corresponde a uma quebra estrutural da série. Para "colar" as duas séries nesse dia optei por tomar como valor do número de infetados nesse dia a média dos valores desse dia com o valor do número de infetados do dia seguinte.

Os gráficos seguintes mostram os dados da série temporal do número de infetados assim como a exponencial que melhor a aproxima e a aproximação logística.

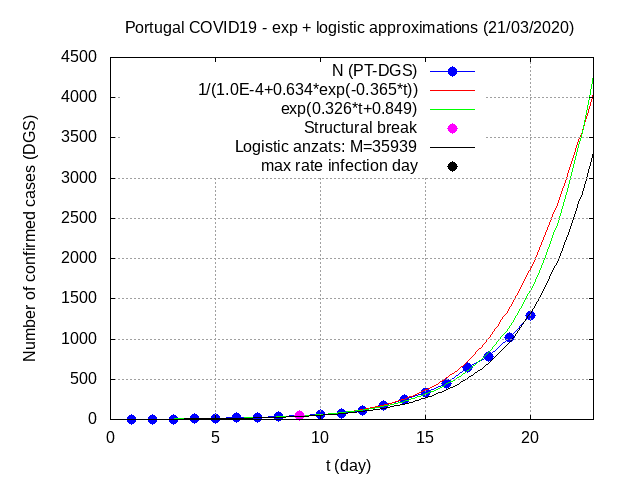
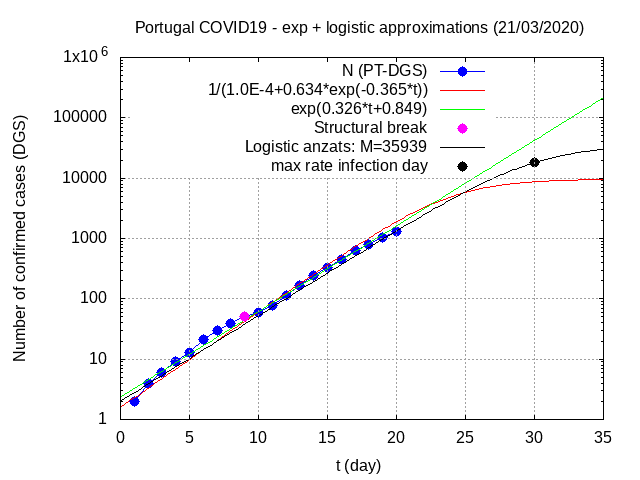
O ajuste exponencial é feito usando a técnica usual de regressão linear com os dados logaritimizados. A aproximação logística requer alguma explicação mais detalhada. É baseada num artigo⁴ de Mar-Molinero de 1980 sobre o stock de tratores agricolas em Espanha. É uma estimativa analítica e que serve como base para previsões com técnicas mais robustas e fiáveis.

A técnica usada por Molinero é chamada técnica dos três pontos e tem uma receita simples. Depois de invertidos os valores numéricos da série temporal, a inversão da série permite simplificar as contas ;),

     1
Y = --- = a + b*r^t
     y

fazemos 3 grupos com o mesmo número (ímpar) de elementos. Fazemos a média em cada um desses conjuntos e.g. 3 pontos do início da série, 3 a "meio" e 3 no fim, a saber R, S e T.

n:lmax(matrix_size(y))$
M:lmax(makelist(y[i][2],i,n))$
Y:makelist(1/y[i][2],i,n)$

m:3$

R:float(sum(Y[i],i,1,m)/m)$
T:float(sum(Y[n-i],i,0,m-1)/m)$
S:if evenp(n)
  then
  float(sum(Y[n/2+i]/m,i,-(m-1)/2,(m-1)/2))
  else
  float(sum(Y[(n+1)/2+i]/m,i,-(m-1)/2,(m-1)/2))$

E depois admitimos que as três quantidades R, S e T "obedecem à mesma equação logística, o que nos permite obter um sistema linear nas quantidades a e b e uma expressão não linear para r. (Nota: noMaxima log(x) é o logaritmo natural ou neperiano ln(x).)

aux:if evenp(n)then 1 else 0$
r:exp(2/(n-m-aux)*log((T-S)/(S-R)))$

nx:if evenp(n)then n/2 else (n+1)/2$

[ax+bx*(r^((m+1)/2)+r^(n-(m+1)/2+1))/2=(T+R)/2, ax+bx*r^nx=S]$
solab:float(solve(%,[ax,bx]))$
a:(rhs(solab[1][1]))$
b:(rhs(solab[1][2]))$

P(t):=1/(a+b*r^(t))$
k:log(1/r)$
Pe(t):= 1/(a+b*exp(-k*t))$

A taxa de crescimento exponencial k é dada por ln(1/r).

E é isto. Mas vamos então aos ajustes!

A figura seguinte mostra duas curvas, duas funções logísticas.

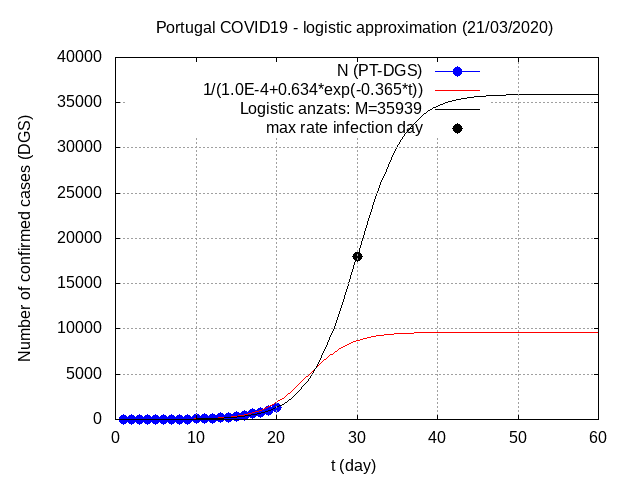
A curva a vermelho é a curva que se obtém usando o algoritmo dos três pontos descrito acima. Faz as seguintes "previsões" com No igual 2.

Número máximo de infetados: 9637
Taxa de crescimento exponencial inicial k: 0.365
Dia de taxa de infeção máxima: 24 dias (a contar do dia 0 - 2/março/2020)
Tempo característico d: 12 dias

A curva preto é também uma logística mas tomando como hipótese que o dia de taxa de infeção máxima será de 30 dias (em linha com os dados de Wuhan) e assumindo a mesma taxa de crescimento exponencial da curva a vermelho e

M = No + No*exp(k*t*)

o que fixa o número máximo de infetados em 35940. O tempo característico para este caso é também 12 dias.

Outra coisa que este tipo de ajustes permite fazer é perceber porque é que o procedimento de restringirmos o contacto físico, e não restrição social, é importante para controlo da epidemia.

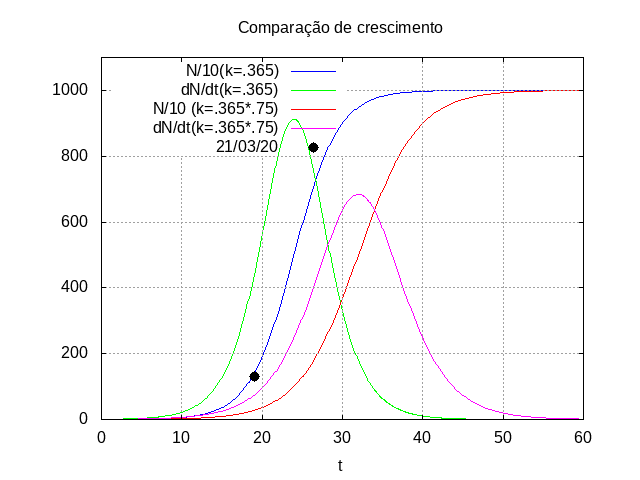
A imagem anterior mostra o ajuste direto logístico a azul (dividido por 10) para os dados com as características anteriores, em particular tem k igual a 0.365. Mostra também a derivada dessa função a verde. A taxa de infeção máxima ocorre no máximo dessa função, no vigésimo quarto dia. Nesse dia o modelo indica que teremos uma taxa de infetados de 900/dia.

A curva a vermelho mostra o ajuste que se obtém mantendo o valor final máximo de infetados (dividido por 10) mas reduzindo a taxa inicial de crescimento exponencial para 75% do seu valor atual. A derivada está a magenta.

O que a comparação destas funções mostra é que apesar de se ter o mesmo número final máximo de infetados a escala temporal onde se desenvolve a epidemia é diferente.

Obviamente que essa escala é mais dilatada no caso em que a taxa de crescimento exponencial é mais baixa, mas mostra também que em vez de termos cerca de 900 infetados por dia teremos agora cerca de 700/dia e sete dias depois. Mostra também que a escala temporal característica do primeiro caso, 12, é dois terços menor que a escala da segunda que é 16, dando um pouco de mais tempo ao Serviço Nacional de Saúde de preparar os cuidados a um fluxo menor de necessidades garantindo o alívio necessário à manutenção dos cuidados de saúde à população.

Como é fácil de perceber, e apesar deste modelo não ser o mais relevante para fazer previsões, é no entanto um bom ajuste e serve para ganharmos alguma sensibilidade na compreensão de um fenómeno natural que é uma epidemia. Não podemos controlar drasticamente o resultado final mas podemos controlar os tempos e a dinâmica em que o fenómeno se desenvolve.

É por isso que é preciso que não te fiques pelos ajustes. Fica em casa!

1. O código para gerar o gráfico em Maxima é este:

plot2d([exp(.1*t),62/(1+(62-1)*exp(-.1*t))],
  [t,0,100],[y,0,100],
  [title,"Comparação de crescimento"],
  [xlabel, "t"],
  [ylabel, "N"],
  [style, lines,lines],
  [point_type,bullet,bullet,bullet],
  [color, blue, red],
  [legend, "exponencial", "logística"],
  grid2d)$

2. H. G. Thornton, On the development of a standardized agar medium for counting soil bacteria, Ann. Appl. Biol., 9:241-274, (1922)

3. É uma equação de variáveis separáveis e basta uma primitivação de uma função racional ;)

4. C. Mar-Molinero, Tractors in Spain: A Logistic Analysis, The Journal of the Operational Research Society, Vol. 31, No. 2, pp. 141-152 (1980)

Criado/Created: 20-03-2020 [00:23]

Última actualização/Last updated: 14-02-2024 [10:25]

Voltar à página inicial.