Onde está o Wallis?

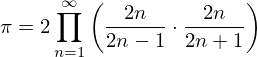
A fórmula de Wallis é dada por¹ $latex2png equation$

O código seguinte implementa em LISP a fórmula de Wallis de uma forma recursiva

(defun wallis(n)
  (cond ((eq n 0)
         2)
        (t
         (* (/ (* 2 n) (- (* 2 n) 1))
            (wallis (- n 1))
            (/ (* 2 n) (+ (* 2 n) 1))))))

Não deixa de ser curioso os diferentes outputs para vários valores de n:

> (wallis 1)
8/3

> (wallis 2)
128/45

> (wallis 3)
512/175

> (wallis 4)
32768/11025

> (wallis 5)
131072/43659

> (wallis 10)
137438953472/44801898141

> (wallis 50)
50216813883093446110686315385661331328818843555712276103168/16063834434771661191161473607166722989851247353354683757549

> (wallis 100)
80695308690215893426747474125094121072803306025913234775958104891895238188026287332176417290004307232371974124148359168/25750089606120885825398316830453602944399672486522403084160282339703753666964959026911303870016475450552576115105122225

Ou numa versão em vírgula flutuante:

(defun wallis-fp(n)
  (cond ((eq n 0)
         2)
        (t
         (* (/ (* n n) (- (* n n) .25))
            (wallis-fp (- n 1))))))

> (wallis-fp 1)
2.6666667

> (wallis-fp 2)
2.8444448

> (wallis-fp 3)
2.9257147

> (wallis-fp 4)
2.9721549

> (wallis-fp 5)
3.0021765

> (wallis-fp 10)
3.067705

> (wallis-fp 50)
3.1260788

> (wallis-fp 100)
3.1337879

> (wallis-fp 1000)
3.1408064

> (wallis-fp 10000)

3.1413496

Divirtam-se!

1. Por causa disto ;) New Derivation of Pi Links Quantum Physics and Pure Math

Created: 20-11-2015 [11:02]

Last updated: 23-01-2025 [00:04]

For attribution, please cite this page as:

Charters, T., "Onde está o Wallis?": https://nexp.pt/OndeEstaOWallis.html (23-01-2025 [00:04])

(cc-by-sa) Tiago Charters - tiagocharters@nexp.pt